Giải bài tập Toán 7 Bài tập cuối chương 1 trang 25
Video giải bài tập Toán 7 Bài tập cuối chương 1 trang 25
Giải Toán 7 trang 25 Tập 1
Bài 1.35 trang 25 Toán 7 Tập 1: Hình 1.14 mô phỏng vị trí của năm điểm A, B, C, D, E so với mực nước biển. Biết rằng độ cao (tính theo đơn vị kilômét) so với mực nước biển của mỗi điểm là một trong các số sau: 3312; 7930; −2512; −56; 0.
Quan sát hình và cho biết độ cao của mỗi điểm.
![]()
Lời giải:
Quan sát Hình 1.14 ta thấy:
+) Điểm A và điểm B ở bên trên mực nước biển nên độ cao so với mực nước biển của hai điểm A và điểm B là hai số dương. Điểm A nằm bên dưới điểm B nên độ cao của điểm A thấp hơn độ cao của điểm B.
Xét hai số hữu tỉ dương: 3312;7930.
Ta có 3312=16560; 7930=15860.
Vì 165 > 158 nên 16560>15860 hay 3312>7930.
Vậy độ cao của điểm A là 7930, độ cao của điểm B là 3312.
+) Điểm C nằm trùng với mực nước biển nên độ cao so với mực nước biển của điểm C là 0.
Vậy độ cao của điểm C là 0.
+) Điểm D và điểm E ở bên dưới mực nước biển nên độ cao so với mực nước biển của hai điểm D và điểm E là hai số âm. Điểm D nằm bên dưới điểm E nên độ cao của điểm D thấp hơn độ cao của điểm E.
Xét hai số hữu tỉ âm: −2512; −56
Ta có −56=−1012;−2512=−2512
Vì -25 < -10 nên −2512<−1012 hay −2512< −56.
Vậy độ cao của điểm D là −2512 độ cao của điểm E là −56.
Bài 1.36 trang 25 Toán 7 Tập 1: Tính giá trị của các biểu thức sau:
a) 312+3151+33;
b) 2:12−232+0,1253.83−−124:64.
Lời giải:
a) 312+3151+33
=312+312+31+33
=312+312.331+33
=312.1+331+33
=312
Vậy 312+3151+33=312.
b) 2:12−232+0,1253.83−−124:64.
=2:36−462+0,125.83−−12464
=2:−162+13−−12464
=2:−1262+1−−1264
= 2.62 + 1 - (- 2)4
= 2.36 + 1 - 16
= 72 + 1 - 16
= 73 - 16
= 57.
Vậy 2:12−232+0,1253.83−−124:64=57.
Bài 1.37 trang 25 Toán 7 Tập 1:
Chị Trang đang có ba tháng thực tập tại Mỹ. Gần hết thời gian thực tập, chị Trang và bạn có kế hoạch tổ chức một bữa tiệc chia tay trước khi về nước. Chị ấy dự định mua 4 cái bánh pizza, mỗi cái giá 10,25 USD. Chị Trang có phiếu giảm giá 1,5 USD cho mỗi cái bánh pizza, hãy tính tổng số tiền chị ấy dùng để mua bánh.
Lời giải:
Số tiền chị Trang dùng để mua 1 cái bánh pizza khi dùng phiếu giảm giá là:
10,25 - 1,5 = 8,75 (USD).
Tổng số tiền chị Trang dùng để mua 4 cái bánh pizza sau khi dùng phiếu giảm giá là:
4.8,75 = 35 (USD).
Vậy chị Trang dùng hết 35 USD để mua 4 cái pizza.
Bài 1.38 trang 25 Toán 7 Tập 1: Bố của Hà chuẩn bị đi công tác bằng máy bay. Theo kế hoạch, máy bay sẽ cất cánh lúc 14 giờ 40 phút. Bố của Hà cần phải có mặt ở sân bay trước ít nhất 2 giờ để làm thủ tục, biết rằng đi từ nhà Hà đến sân bay mất khoảng 45 phút. Hỏi bố của Hà phải đi từ nhà muộn nhất là lúc mấy giờ để đến sân bay cho kịp giờ bay?
Lời giải:
Tổng thời gian bố Hà cần di chuyển từ nhà đến sân bay và làm thủ tục trước khi bay là:
2 giờ + 45 phút = 2 giờ 45 phút.
Đổi 14 giờ 40 phút = 13 giờ 100 phút.
Để kịp cho chuyển bay cất cánh lúc 14 giờ 40 phút thì bố của Hà phải đi từ nhà muộn nhất là lúc:
13 giờ 100 phút - 2 giờ 45 phút = 11 giờ 55 phút.
Vậy bố của Hà phải đi từ nhà muộn nhất là lúc 11 giờ 55 phút để đến sân bay cho kịp giờ bay.
Lý thuyết Toán 7 Ôn tập chương 1 - Kết nối tri thức
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số
• Số hữu tỉ là số viết được dưới dạng phân số ab với a, b ∈ ℤ, b ≠ 0.
Tập hợp các số hữu tỉ được kí hiệu là ℚ.
• Cách biểu diễn số hữu tỉ ab trên trục số:
+ Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.
+ Điểm biểu diễn số hữu tỉ ab cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).
Ví dụ 1:
+ Các số - 7; 0,3; - 234 là các số hữu tỉ vì chúng viết được dưới dạng phân số: - 7 = −71; 0,3 = 310; - 234 = −114.
+ Biểu diễn số hữu tỉ 32 trên trục số ta làm như sau:
Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).
Số hữu tỉ 32 được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)
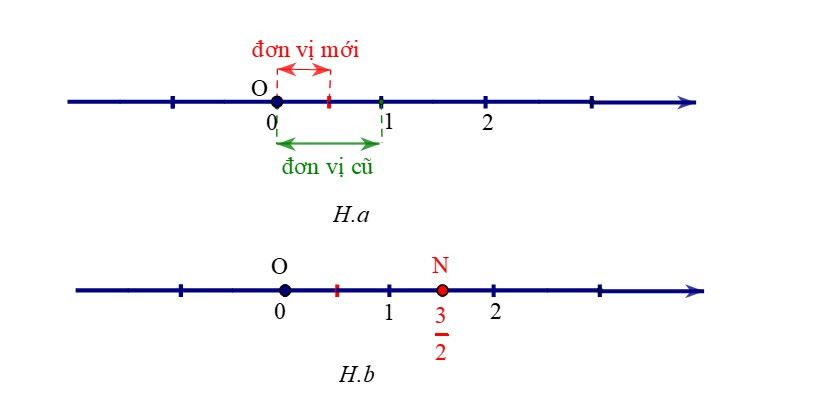
+ Số đối của số hữu tỉ 32 là số hữu tỉ −32 được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.
Chú ý:
• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ - m.
• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.
• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.
Ví dụ 2: Số đối của các số hữu tỉ sau: −9,7; 358; −12; 6.
Hướng dẫn giải
Số đối của 0 - 9,7 là - (- 9,7) = 9,7;
Số đối của 358 là −358;
Số đối của −12 là −−12=12;
Số đối của 6 là - 6.
2. Thứ tự trong tập hợp các số hữu tỉ
• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.
• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.
Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).
• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.
Ví dụ:
+ So sánh 0,5 và 34 ta làm như sau:
Ta có 0,5 = 510=12=24
Vì 2 < 3 nên 24 < 34 hay 0,5 < 34.
+ 0,5 < 34 nên 0,5 nằm trước 34 trên trục số.
+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ 56 và 65 như sau:
Vì 56<66=1 và 1=55<65 nên 56 < 1 < 65.
Vậy 56<65.
Chú ý:
• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
3. Cộng và trừ hai số hữu tỉ
Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
Ví dụ 1: Tính:
a) −618+1827;
b) - 0,32 + 0,98;
c) - 5 + 215.
Hướng dẫn giải
a) −618+1827=−13+23=−1+23=13;
b) - 0,32 + 0,98 = 0,98 - 0,32 = 0,66;
c) - 5 + 215 = −255+115=−25+115=−145.
Chú ý:
• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.
• Trong phép cộng trừ với số hữu tỉ ℚ, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên ℤ.
• Đối với một tổng trong ℚ, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong ℤ.
• Hai số đối nhau luôn có tổng bằng 0:
a + (- a) = 0.
Ví dụ 2: Thực hiện phép tính
a) 2−3+−56+13+116;
b) 313−12−23−12.
Hướng dẫn giải
a) 2−3+−56+13+116
=−23+−56+13+76 (Viết số hữu tỉ dưới dạng phân số có mẫu dương)
=−23+13+−56+76 (Tính chất giao hoán)
=−23+13+−56+76 (Tính chất kết hợp)
=−13+26
=−13+13=0 (Tổng hai số đối nhau bằng 0)
b) 313−12−23−12
=313−12−23+12 (Quy tắc bỏ dấu ngoặc có dấu “-” đằng trước)
=313−23+−12+12 (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)
=293+0=293 (Cộng với số 0)
4. Nhân và chia hai số hữu tỉ
• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
Chú ý:
• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.
• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.
Ví dụ 1: Tính:
a) 233⋅646⋅−910;
b) −76:157;
c) 76⋅314+76⋅−0,25.
Hướng dẫn giải
a) 233⋅646⋅−910
=233⋅323⋅−910
=1⋅−910=−910 (Nhân với số 1)
b) −76:157
=−76:127
=−76⋅712=−4972
c) 76⋅314+76⋅−0,25
=76⋅314+−0,25
=76⋅134+−14
=76⋅124=72
Ví dụ 2: 1,25 . (- 4,6) = - (1,25 . 4,6) = - 5,75.
5. Lũy thừa với số mũ tự nhiên
• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xn, là tích của n thừa số x (n là số tự nhiên lớn hơn 1)
xn=x⋅x⋅x⋅ ...⋅x⏟n thừa số (x ∈ℚ, n ∈ℕ, n >1)
xn đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.
x gọi là cơ số, n gọi là số mũ.
Quy ước: x0 = 1 (x ≠ 0); x1 = x.
Ví dụ:
+ 53 đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.
+ Tính −134
−134=−13⋅−13⋅−13⋅−13=−1⋅−1⋅−1⋅−13⋅3⋅3⋅3=181
+ Tính và so sánh: 12262 và −1262
12262=14436=4 và −1262=−22=4 nên 12262=−1262
Chú ý:
• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.
x⋅yn=xn⋅yn; xyn=xnyn (y ≠ 0).
Ví dụ:
3415.415=34.415=315;
253 : 53 = 2553=53=125.
6. Nhân và chia hai lũy thừa cùng cơ số
• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.
xm⋅xn=xm+n
• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.
xm:xn=xm−n (x ≠ 0, m ≥ n)
Ví dụ:
+ Tính 232.235
232.235=232+5=237=1282187
+ Tính −95:−94
−95:−94=−95−4=−91=−9.
7. Lũy thừa của lũy thừa
• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.
xmn=xm⋅n
Ví dụ:
+ Tính −357
−357=−35⋅7=−335.
Mở rộng
• Lũy thừa với số mũ nguyên âm của một số khác 0.
x−n=1xn với n là số nguyên dương, x ≠ 0.
Ví dụ: 1100=1102=10−2
8. Thứ tự thực hiện các phép tính
• Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực hiện các phép tính theo thứ tự từ trái sang phải.
• Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:
• Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
→→
Ví dụ: Tính giá trị của biểu thức:
a) 1,5 - 23 + 7,5 : 3;
b) 32:111−522+74⋅114−27.
Hướng dẫn giải:
a) 1,5 - 23 + 7,5 : 3
= 1,5 - 8 + 2,5 (Thực hiện lũy thừa; nhân chia trước)
= - 6,5 + 2,5 = - 4
b) 32:111−522+74⋅114−27
=32:−322+74⋅−314 (Thực hiện trong ngoặc trước)
=32⋅−223+−38 (Thực hiện nhân chia trước)
=−11+−38=−918.
9. Quy tắc chuyển vế
• Đẳng thức có dạng A = B. Trong đó A là vế trái; B là vế phải của đẳng thức.
Ví dụ: 4,1 + x = 2,3 là một đẳng thức, trong đó 4,1 + x là vế trái, 2,3 là vế phải.
• Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:
Nếu a = b thì: b = a; a + c = b + c.
• Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “-” và dấu “-” đổi thành dấu “+”.
+) Nếu a + b = c thì a = c - b;
+) Nếu a - b = c thì a = c + b.
Ví dụ: Tìm x, biết:
a) x+13=−57;
b) x−54=98.
Hướng dẫn giải
a) x+13=−57
x=−57−13 (Quy tắc chuyển vế)
x=−1521−721
x=−2221
Vậy x=−2221.
b) x−54=98
x=98+54 (Quy tắc chuyển vế)
x=98+108
x=198
Vậy x=198.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 5: Làm quen với số thập phân vô hạn tuần hoàn
Bài 6: Số vô tỉ. Căn bậc hai số học
Bài 7: Tập hợp các số thực
Luyện tập chung trang 37, 38
Bài tập cuối chương 2 trang 39
Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Ôn tập chương 1


