Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 2: Tứ giác chi tiết sách Toán 8 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 2: Tứ giác
Giải Toán 8 trang 63 Tập 1
Khởi động trang 63 Toán 8 Tập 1: Hình màu xanh bên được trích ra từ bản đồ được gọi là Tứ giác Long Xuyên. Em hãy cho biết:
‒ Hình này được tạo bởi mấy đoạn thẳng?
‒ Các đoạn thẳng này nối các địa điểm nào?
Lời giải:
‒ Hình trên được tạo bởi 4 đoạn thẳng (CH, HR, RL, LC).
‒ Các đoạn thẳng này nối các địa điểm C (Châu Đốc), H (Hà Tiên), Q (Rạch Giá), L (Long Xuyên).
1. Tứ giác
Khám phá 1 trang 63 Toán 8 Tập 1: Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?
Lời giải:
Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1, hình a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.
Giải Toán 8 trang 64 Tập 1
Khám phá 2 trang 64 Toán 8 Tập 1: Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.
Lời giải:
Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:
Nhận xét:
• Hình a): các cạnh còn lại của tứ giác luôn nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.
• Hình b): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.
• Hình c): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.
Giải Toán 8 trang 65 Tập 1
Thực hành 1 trang 65 Toán 8 Tập 1: Vẽ tứ giác MNPQ và tìm:
‒ Hai đỉnh đối nhau;
‒ Hai đường chéo;
‒ Hai cạnh đối nhau.
Lời giải:
Trong tứ giác MNPQ có:
‒ Hai đỉnh đối nhau: M và P; N và Q;
‒ Hai đường chéo: MP và NQ;
‒ Hai cạnh đối nhau: MN và PQ; MQ và NP.
Vận dụng 1 trang 65 Toán 8 Tập 1: Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).
Lời giải:
Trong tứ giác Long Xuyên CHRL có:
• Các đỉnh: C, H, R, L;
• Các cạnh: CH, HR, RL, LC;
• Các đường chéo: CR và HL.
2. Tổng các góc của một tứ giác
Khám phá 3 trang 65 Toán 8 Tập 1: Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?
Lời giải:
• Xét DACB có: BAC^+ABC^+ACB^=180° (định lí tổng ba góc trong một tam giác).
Xét DACD có: CAD^+ACD^+ADC^=180° (định lí tổng ba góc trong một tam giác).
Do đó BAC^+ABC^+ACB^+CAD^+ACD^+ADC^=180°+180°=360°.
Vậy tổng các góc của tam giác ACB và tam giác ACD bằng 360°.
• Ta có: BAC^+ABC^+ACB^+CAD^+ACD^+ADC^=360°
Suy ra BAC^+CAD^+ABC^+ACB^+ACD^+ADC^=360°
Hay A^+B^+C^+D^=360°.
Vậy tổng các góc của tứ giác ABCD bằng 360°.
Giải Toán 8 trang 66 Tập 1
Thực hành 2 trang 66 Toán 8 Tập 1: Tìm x trong mỗi tứ giác sau:
Lời giải:
• Hình 9a):
Xét tứ giác PQRS có: 80° + 70° + 2x + x = 360° (định lí tổng các góc của một tứ giác)
Suy ra 3x = 360° - (80° + 70°) = 210°
Do đó x = 70°.
• Hình 9b):
Xét tứ giác ABCD có: x + 95° + 100° + 90° = 360° (định lí tổng các góc của một tứ giác)
Suy ra x = 360° - (95° + 100° + 90°) = 75°.
• Hình 9c):
Xét tứ giác EFGH có: 99° + 90° + 90° + x = 360° (định lí tổng các góc của một tứ giác)
Suy ra x = 360° - (99° + 90° + 90°) = 81°.
Vận dụng 2 trang 66 Toán 8 Tập 1: Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.
Lời giải:
Xét DABC và DADC có:
AC là cạnh chung; AB = AD; BC = DC (giả thiết).
Do đó DABC = DADC (c.c.c).
Suy ra B^=D^ (hai góc tương ứng).
Xét tứ giác ABCD có: A^+B^+C^+D^=360° (định lí tổng các góc của một tứ giác)
Suy ra 130°+B^+60°+B^=360°
Hay 2B^=360°−130°+60°=170°.
Do đó B^=85°.
Vậy B^=D^=85°.
Bài tập
Bài 1 trang 66 Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.
Lời giải:
• Hình 11a):
Xét tứ giác ABCD có: A^+B^+C^+D^=360° (định lí tổng các góc của một tứ giác)
Suy ra B^=360°−A^+C^+D^
Hay B^=360°−110°+75°+75°=100°.
• Hình 11b):
Xét tứ giác MNPQ có: M^+N^+P^+Q^=360° (định lí tổng các góc của một tứ giác)
Suy ra M^=360°−N^+P^+Q^
Hay M^=360°−90°+90°+70°=110°.
• Hình 11c):
Ta có TSV^=180°−60°=120° (do TSV^ kề bù với góc có số đo bằng 60°)
Xét tứ giác STUV có: TSV^+T^+U^+V^=360° (định lí tổng các góc của một tứ giác)
Suy ra V^=360°−TSV^+T^+U^
Hay V^=360°−120°+65°+115°=60°.
• Hình 11d):
Xét tứ giác EFGH có: E^+F^+G^+H^=360° (định lí tổng các góc của một tứ giác)
Suy ra F^=360°−E^+G^+H^
Hay F^=360°−80°+70°+100°=110°.
Bài 2 trang 66 Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài của tứ giác ABCD ở Hình 12.
Lời giải:
Xét tứ giác ABCD có: A^2+B^2+C^2+D^2=360° (định lí tổng các góc của một tứ giác)
Mặt khác: A^1+A^2=180° (hai góc kề bù)
Tương tự: B^1+B^2=180°; C^1+C^2=180°; D^1+D^2=180°
Suy ra
A^1+A^2+B^1+B^2+C^1+C^2+D^1+D^2=180°+180°+180°+180°
Hay A^1+B^1+C^1+D^1+A^2+B^2+C^2+D^2=720°
Do đó A^1+B^1+C^1+D^1+360°=720°
Nên A^1+B^1+C^1+D^1=720°−360°=360°.
Vậy tổng số đo bốn góc ngoài A^1,B^1,C^1,D^1 của tứ giác ABCD bằng 360°.
Giải Toán 8 trang 67 Tập 1
Bài 3 trang 67 Toán 8 Tập 1: Tứ giác ABCD có A^=100°, góc ngoài tại đỉnh B bằng 110°, C^=75°. Tính số đo góc D
Lời giải:
Do góc ngoài tại đỉnh B có số đo bằng 110° nên ABC^=180°−110°=70°.
Xét tứ giác ABCD có: A^+ABC^+C^+D^=360° (định lí tổng các góc của một tứ giác)
Suy ra D^=360°−A^+ABC^+C^
Do đó D^=360°−100°+70°+75°=115°.
Bài 4 trang 67 Toán 8 Tập 1: Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65°, góc ngoài tại đỉnh B bằng 100°, góc ngoài tại đỉnh C bằng 60°. Tính số đo góc ngoài tại đỉnh D.
Lời giải:
Gọi A^1,B^1,C^1,D^1 lần lượt là các góc ngoài tại đỉnh A, đỉnh B, đỉnh C, đỉnh D (hình vẽ).
Áp dụng kết quả của Bài tập 2, trang 66 Sách giáo khoa Toán 8, Tập một cho tứ giác ABCD ta có: A^1+B^1+C^1+D^1=360°
Suy raD^1=360°−A^1+B^1+C^1
Do đó D^1=360°−65°+100°+60°=135°
Vậy góc ngoài tại đỉnh D có số đo bằng 135°.
Bài 5 trang 67 Toán 8 Tập 1: Tứ giác ABCD có số đo A^=x,B^=2x,C^=3x,D^=4x. Tính số đo các góc của tứ giác đó
Lời giải:
Xét tứ giác ABCD có: A^+B^+C^+D^=360° (định lí tổng các góc của một tứ giác)
Suy ra x + 2x + 3x + 4x = 360°
Hay 10x = 360°
Do đó x = 36°.
Khi đó: A^=36°;B^=2.36°=72°;C^=3.36°=108°;D^=4.36°=144°.
Vậy A^=36°;B^=72°;C^=108°;D^=144°.
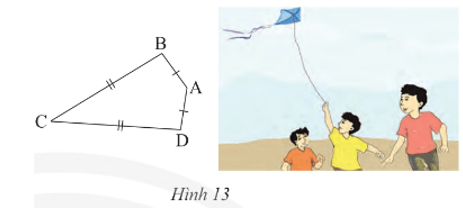
Bài 6 trang 67 Toán 8 Tập 1: Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của BD.
b) Cho biết B^=95°, C^=35°. Tính A^ và D^.
Lời giải:
a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.
Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.
Do đó AC là đường trung trực của đoạn thẳng BD.
b) Xét DABC và DADC có:
AC là cạnh chung; AB = AD; BC = DC (giả thiết).
Do đó DABC = DADC (c.c.c).
Suy ra B^=D^ (hai góc tương ứng).
Mà B^=95° nên D^=95°.
Xét tứ giác ABCD có: A^+B^+C^+D^=360° (định lí tổng các góc của một tứ giác)
Suy ra A^=360°−B^+C^+D^
Do đó A^=360°−95°+35°+95°=135°.
Vậy A^=135° và D^=95°.
Bài 7 trang 67 Toán 8 Tập 1: Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối của cạnh BD.
b) Tìm các đường chéo của tứ giác.
Lời giải:
a) Tứ giác BDNQ có:
• Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB;
• Các cạnh đối: BD và NQ; DN và BQ.
b) Tứ giác BDNQ có các đường chéo BN và DQ.
Video bài giảng Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo
Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Định lí Pythagore
Bài 2: Tứ giác
Bài 3: Hình thang - Hình thang cân
Bài 4: Hình bình hành - Hình thoi
Bài 5: Hình chữ nhật - Hình vuông
Lý thuyết Tứ giác
1. Khái niệm
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ:
Đặc điểm
+Có 4 đỉnh
+ Có 4 cạnh
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất
+Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng 3600.
Tứ giác ABCD, A^+B^+C^+D^=3600
Ví dụ:
B^=3600−930−1230−750=690